HD 钱包的普通子钱包创建算法与不安全性的简单介绍 —— 对《精通比特币》第五章的补充

起因

在阅读 《精通比特币》第二版 第五章 钱包 的时候，发现扩展父私钥创建子私钥与扩展父公钥以创建子公钥的两图中，HMAC-SHA512 的三个输入是完全相同的，都为父公钥、父链码和索引号，并且将结果的左 256 位分别作为了子私钥与子公钥。对于这两张图，我就产生了几个疑惑：

• 为什么用相同的参数生成的两个相同的数在两个场景中可以分别作为私钥和公钥？
• 图上父私钥、父公钥到子私钥、子公钥的连线是什么意思？
• 如果子私钥和子公钥不同，如何能确保它们是配对的？

后来发现这些问题都源于漏看文章的几句话以及文章没有对算法进行详述。（捂脸

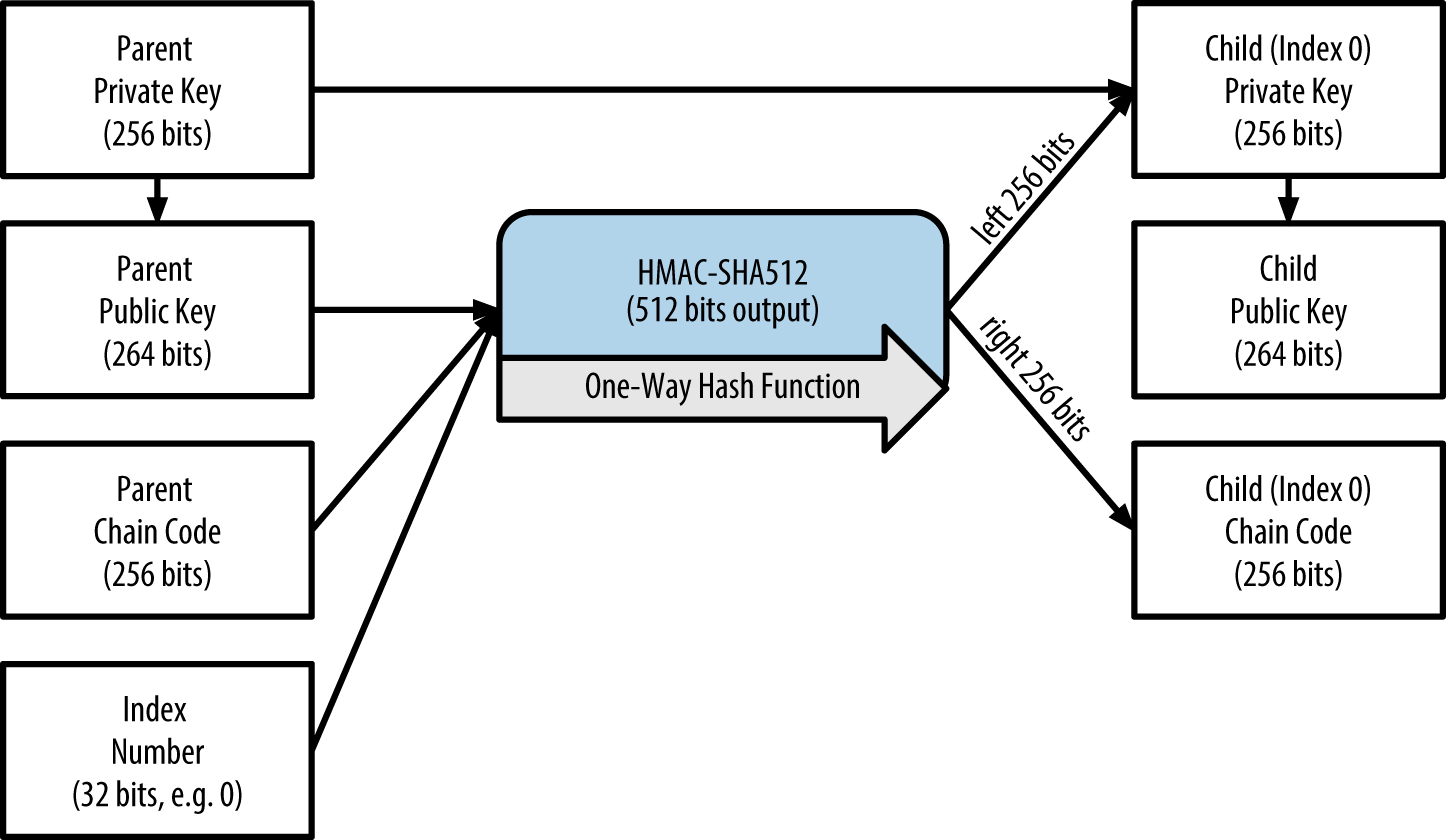
扩展父私钥创建子私钥

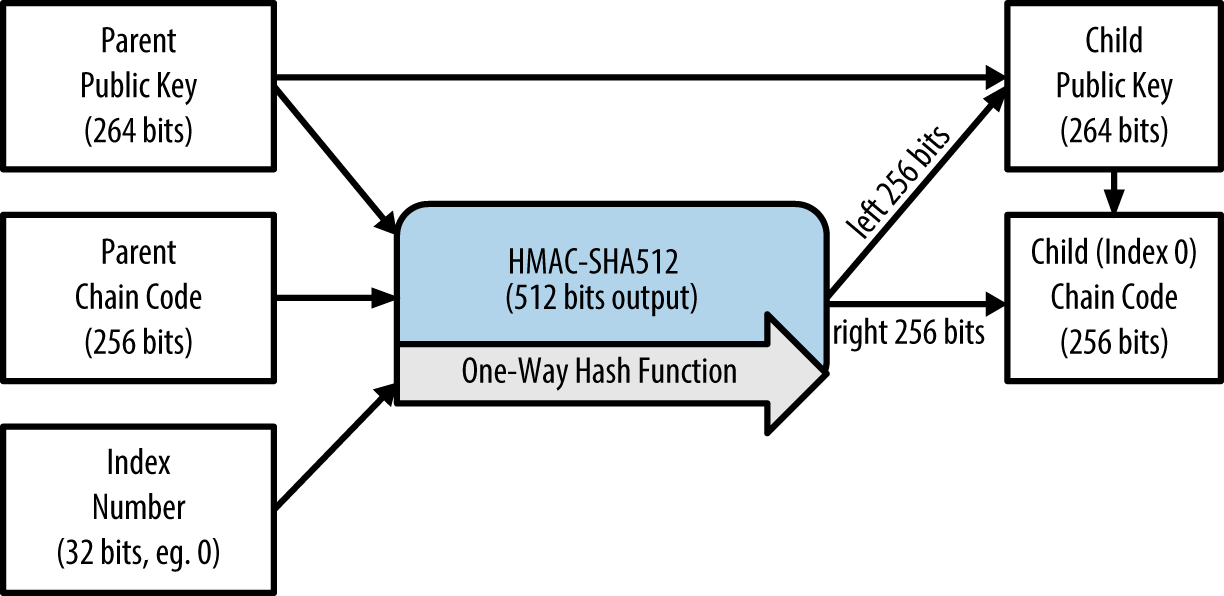
扩展父公钥以创建子公钥

子私钥 / 公钥生成算法

本文所涉及的规范是 BIP32，这里不考虑 hardened key 的情况，只考虑普通子密钥的生成。更详细的算法及说明请看知识学堂 | HD 钱包详解：Part 2 BIP32 注解（存档）中的相关内容。

相关符号：

• $c_{par}$ 父链码
• $k_{par}$ 父私钥
• $K_{par}$ 父公钥（即大写 K 为公钥，小写 k 为私钥）
• $i$ 子密钥序号（索引）
• $point(p)$ 返回 $p\ast G$ 的坐标对，即：将 $p$ 看作私钥，则 $point(p)$ 就是对应的公钥
• $se{r}_{32}(i)$ 将一个 32 位的无符号位整数 i 序列化为一个 4 字节的序列，大端规则
• $se{r}_P(P)$ 序列化点 P
• $pars{e}_{256}(p)$ 将一个 32 字节的序列解析（反序列化）为一个 256 位的数，大端规则

父私钥 -> 子私钥：

1. $I=HMAC-SHA512(Key=c_{par},Data=se{r}_P(point(k_{par}))||se{r}_{32}(i))$，即：用父公钥、父链码、索引号生成 HMAC-SHA512 后的哈希
2. 将 $I$ 均分为左右两部分 $I_L$ 和 $I_R$
3. 子私钥 $k_i=pars{e}_{256}(I_L)+k_{par}(modn)$ ，即：子私钥是由 $I_L$ 与父私钥 (mod n 后) 相加而成的，这也解释了上图中顶部父私钥到子私钥的连线的含义
4. 子链码 $c_i=I_R$

父公钥 -> 子公钥：

1. $I=HMAC-SHA512(Key=c_{par},Data=se{r}_P(K_{par})||se{r}_{32}(i))$，和上面父私钥 -> 子私钥算法中的步骤一对比，由于 $K_{par}=point(k_{par})$，因此事实上两者的结果就是相同的，并且这是保证两种算法生成的子密钥能配对的前提
2. 将 $I$ 均分为左右两部分 $I_L$ 和 $I_R$
3. 子公钥 $K_i=point(pars{e}_{256}(I_L))+K_{par}$ 注意这里的加法不是数值相加，而是椭圆曲线上的点的加法（因为加号左右两边都是椭圆曲线上的点）
4. 子链码 $c_i=I_R$

子公钥与子私钥匹配证明

由于 父私钥 -> 子私钥 与 父公钥 -> 子公钥 算法中的 I 是完全一致的，所以拆分得到的子链码也是相同的，并且 $I_L$ 也是相同的。

因此，由父私钥推导出的子公钥为

$$\begin{array}{rl}{K}_i& =point(k_i)\\ & =point(pars{e}_{256}(I_L)+k_{par}(modn))\\ & =point(pars{e}_{256}(I_L))+point(k_{par}(modn))\\ & =point(pars{e}_{256}(I_L))+K_{par}\end{array}$$

与由父公钥推导得出的子公钥相同，因此它们是相互配对的。其中第二步到第三步是因为椭圆曲线上的点的乘法运算满足分配律。

不安全性证

文章中也提到，泄露的子私钥 ($k_i$) 加上 xpub (即 $K_{par}$ 与 $c_{par}$)，可以用来推断父私钥 ($k_{par}$)，推断方式如下：

$$\begin{array}{rl}& k_i=pars{e}_{256}(I_L)+k_{par}(modn)\\ =>& k_{par}=k_i-pars{e}_{256}(I_L)\end{array}$$

根据 xpub 可以生成 $I_L$，已知 $k_i$，即可计算出 $k_{par}$.

参考资料

1. 《精通比特币》第二版 第五章 钱包
2. 知识学堂 | HD 钱包详解：Part 2 BIP32 注解（存档）